Just a cute Python snippet I put together today and thought worth sharing. Needed to fill in a matrix in from the corner outwards, iterating down successive diagonals. You might also run into this problem doing a zigzag traversal of a nested list-of-lists.

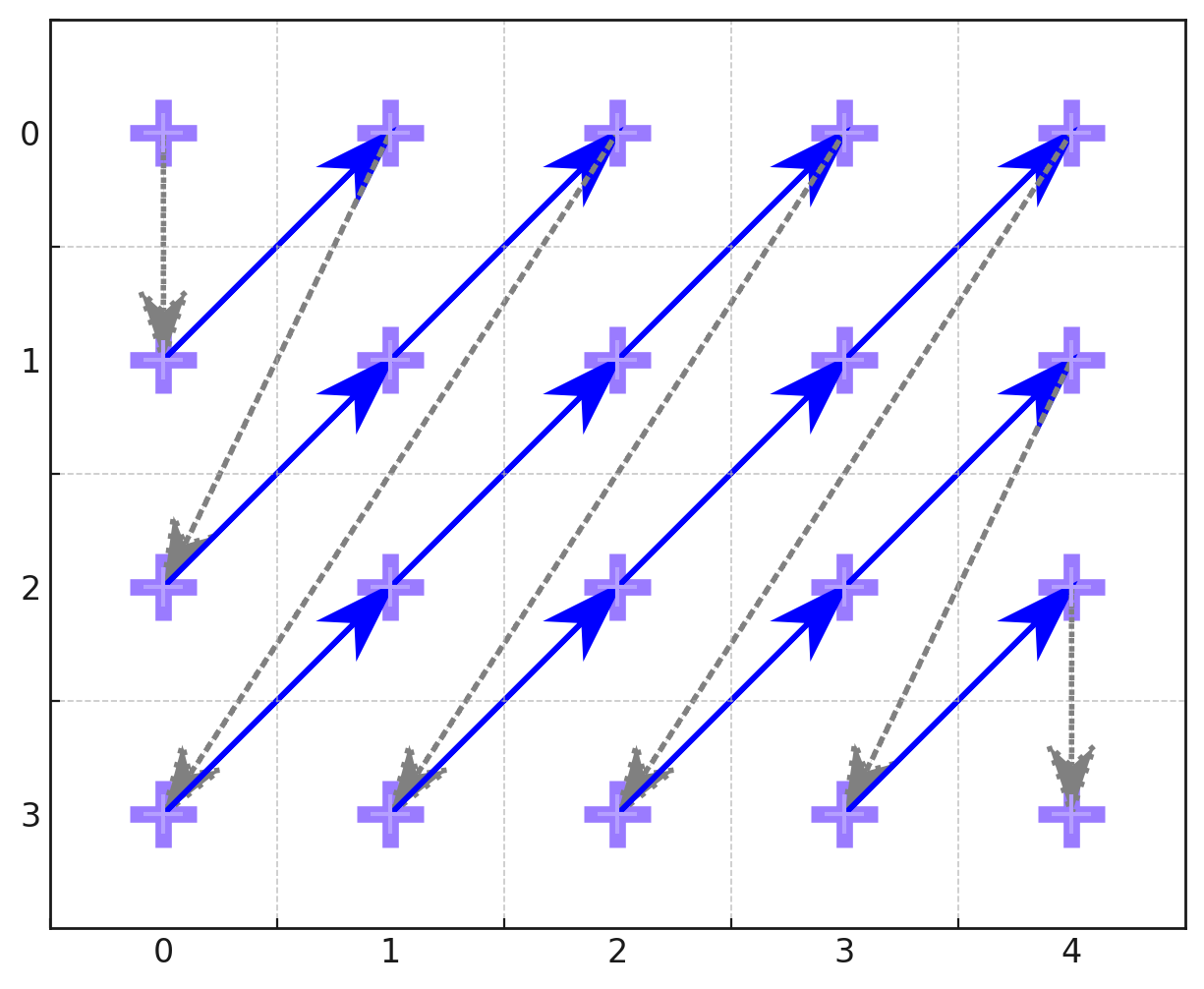
zig-zag traversal over a 3x4 grid

Itertools comes to the rescue with a nice one liner to generate the (row, col) coordinate sequence.

🔗 Ctrl-C Ctrl-V

For a dimxdim square matrix,

sorted(itertools.product(range(dim), repeat=2), key=sum)

In the arbitrary nrowxncolcase,

sorted(itertools.product(range(nrow), range(ncol)), key=sum)

🔗 How does this work?

In iterating over the matrix, we want to see all combinations of row and column indices — this is a product. Sort by (row, col) coordinate sums to get ascending diagonals. For example, (0, 0) has sum 0 so will be ordered first. The coordinates, (0, 1) and (1, 0) both have sum 1 so will be ordered next.

The stability of sort and the iteration order of product gets us the correct ordering along same-sum diagonals.

🔗 Examples

For a square matrix with dim = 3,

>>> import itertools as it
>>> sorted(it.product(range(3), repeat=2), key=sum)
[(0, 0), (0, 1), (1, 0), (0, 2), (1, 1), (2, 0), (1, 2), (2, 1), (2, 2)]

For a matrix with nrow=2 and ncol=3,

>>> sorted(it.product(range(2), range(3)), key=sum)
[(0, 0), (0, 1), (1, 0), (0, 2), (1, 1), (1, 2)]

🔗 Bonus: Chunked Diagonals

To take successive diagonal coordinate sequences as separate chunks, just group by coordinates’ sums.

>>> import itertools as it
>>> for diagonal, coords in it.groupby(
...     sorted(it.product(range(3), repeat=2), key=sum),
...     key=sum,
...):
...     print(f"{diagonal=}")
...     print("coords=", [*coords], "\n")
...
diagonal=0
coords= [(0, 0)]

diagonal=1
coords= [(0, 1), (1, 0)]

diagonal=2
coords= [(0, 2), (1, 1), (2, 0)]

diagonal=3
coords= [(1, 2), (2, 1)]

diagonal=4
coords= [(2, 2)]